| Turnstyle

Naturally, a casual walk on a stimulating work environment can trigger the most prominent forms of nerd snipping. Another addictive puzzle from the ninth floor dazzled me. Hopefully, I can share some of my curiosity with you.

The Turnstyle brain teaser consists of two discs connected by a gear on the back. Allowing two types of valid moves:

Shift all the numbers one position right (clockwise) or left (counter-clockwise).
Flip the connected gears to change the order of the numbers from ABCD to BADC.

After interacting with the puzzle for a few seconds, I knew my best hope was to write a program to find an optimal solution for me.

Let’s solve it!

Being particularly bad at games, I couldn’t help but think whether I should invest a few hours into it. Naturally, one thought crossed my mind: the imminent fear of a jigsaw puzzle missing a piece. What if someone designed a devilish unsolvable game? Let’s better take one step back, and first prove the solvability of the game.

Digging into math

We build up our intution by introducing a set of definitions. Let us consider $\mathcal{A} = \{1,...,n\}$. We define a permutation $\sigma$ as a function from $\mathcal{A}$ to itself, which is onto and one-to-one. In other words, a reording of the elements of $\mathcal{A}$. Any permutation $\sigma$ can be represented by a set of disjoint cycles, with the interpretation that any consecutive pair $i,j$ indicates that $i$ is mapped to $j$, and any $i$ at the end of a parenthesized cycle maps to $j$ at the start of the same cycle.

For example, the permutation $\sigma : \{1,2,3,4\} \rightarrow \{2,1,4,3\}$ can be denoted as $\sigma = (12)(34)$. In addition, a cycle consisting of only two elements is called a transposition and a cycle of one element (which can be avoided in the cycle notation) is called fixed point. In our case, our permutation is expressed as the product of two transpositions.

We define the order of the permutation is the defined the smallest positive integer $m$ such that $\sigma^m = id$. That is, how many times we should apply the permutation mapping until we obtain the identity map. For example, for the above permutation $\sigma$ the order is $2$.

Regarding the parity of a permutation, using the cycle notation, the permutation is odd if and only if this factorization contains an odd number of even-length cycles. Thus, our permutation $\sigma = (12)(34)$ is even. It is easy to proof that the composition of two even permutation is another even permutation. This will be a useful property for proving the solvability.

The set of all permutations of $\mathcal{A}$ is the symmetric group of $n$ symbols, denoted by $\mathcal{S}_n$. As detailed in this paper, for a group $\mathcal{G}$ a subset $\mathcal{X} \subset \mathcal{G}$ is a generating set for $\mathcal{G}$ if every $g \in \mathcal{G}$ can be written as a product of powers of elements taken from $\mathcal{X}$:

$$ g = x_1^{a_1} x_2^{a_2} \cdots x_r^{a_r} $$,

where $x_i \in \mathcal{X}$ and $a_i \in \Z$. Thus, $\mathcal{X}$ generates $\mathcal{G}$ and is denoted by $\mathcal{G} = \langle \mathcal{X} \rangle$.

Lemma

For any odd integer $n>4$, the permutations $\sigma_1 = (1,2,3,\cdots, n)$ and $\sigma_2 = (1,2)(3,4)$ do not generate $\mathcal{S}_n$. This solves the open question stated here.

Proof

Let us consider odd values of $n>4$. We can easily verify that for odd $n>8$, the permutations $\sigma_1 = (1,2,3,\cdots, n)$ and $\sigma_2 = (1,2)(3,4)$ are both even. Therefore, every composition of these two permutations would result in an even permutation, by the property described above. Thus, it is not possible to generate odd permutations, and ultimately $\mathcal{S}_n$. ∎

Lemma

$$\mathcal{S}_{12} = \langle \sigma_1, \sigma_2 \rangle = \langle (1,2,3,\cdots, 12), (1,2) (3,4) \rangle$$

Proof

Let us define the following permutations using the generators $\sigma_1$ and $\sigma_2$,

\[L = \sigma_1 = (1,2,3,4,5,6,7,8,9,10,11, 12)\] \[R = \sigma_1^{-1} = (12, 11,10, 9, 8, 7, 6, 5, 4, 3, 2, 1)\] \[T = \sigma_2 = (1,2) (3,4)\]

We use the auxiliary composition of permutations,

\[P = TLLLTR\] \[Q = RRTLL\]

Thus, we can verify

\[L T L P Q P^3 T L = (1,2)\]

To conclude, we can generate $\mathcal{S}_{12}$ using the transposition $(1,2)$ and the 12-cycle permutation.∎

In plain words, by using the two valid game moves (flip and shift), we can reach any possible configuration, for the case of $n=12$. Therefore, we can now safely verify the solutions using computer search.

Furthermore, we could use a library for symbolic mathematics such as SymPy to quickly verify our result. The library uses the Schreier–Sims algorithm to compute the order of the generated group.

from sympy.combinatorics import Permutation, PermutationGroup
a = Permutation([[0,1],[2,3]], size = 12)
b = Permutation(0,1,2,3,4,5,6,7,8,9,10,11)
G = PermutationGroup([a,b])
print('Group Order:', G.order()) # 12!

I wanted to take this opportunity to relate Feynman’s famous quote on knowing the name of something. Despite I am nowhere near being a formerly trained mathematician, sometimes one can benefit by knowing the name of some obscure group theory concept in order to tackle a problem and appropriately explore previous research efforts on the field.

Time to code

From an algorithmic point, the problem consists of a graph traversal task. Each node represents each of the cyclic permutation formed by the 12 pieces. In order to restrict our representation of cyclic permutations, we fix the position of “$1$” at the beginning of the tuple, for each node.

Due to the high number of possible nodes (11! states = ~39M) in the connected graph, a naive implementation of DFS would reach maximum recursion limits. Thus, I opted for using BFS, since that would also help answering shortest path queries between any initial state to the solved state.

The only piece missing is the transition function to traverse each node. Since we want to keep the element $1$ as fixed point in the tuple representation, we apply the transformations of the shape $[i\%n, (i+1)\%n, (i+2)\%n, (i+3)\%n ]$ for a valid $i$ ($0\leq i < n$), and the necessary rotations to keep the element $1$ at the beginnning. Throughout this post, we denote this sequence of transformations as move($i$).

import math
import numpy as np
from copy import deepcopy
from collections import deque

def move(state, ix):
    # Copy mutable state variable 
    new_state = state.copy()

    # Swap the elements (ix%n, (ix+1)%n) and (ix+2)%n, (ix+3)%n)
    new_state[ix], new_state[(ix + 1) % n] = (
        new_state[(ix + 1) % n], 
        new_state[ix],
    )
    new_state[(ix + 2) % n], new_state[(ix + 3) % n] = (
        new_state[(ix + 3) % n],
        new_state[(ix + 2) % n],
    )

    # Corner cases for resetting 1 at the beginning of the new state
    if ix == 0 or ix == n - 2:
        new_state = new_state[1:] + [new_state[0]]

    elif ix == n - 3 or ix == n - 1:
        new_state = [new_state[-1]] + new_state[:-1]

    return new_state

We can now run our naive BFS implementation.

# Create a set for visited states 
visited = set()

# Keep track of parent states during traversal for path reconstruction
parent = dict()
parent_idx = dict()

# Intialization of solution state
solution_state = [i+1 for i in range(n)]
initial_state = tuple(solution_state)
visited.add(initial_state)
queue = deque([initial_state]) 
parent[initial_state] = initial_state
parent_idx[initial_state] = -1

# Explore immediate neighbors not visited
while queue:
  current_state = list(queue.popleft())
  current_state_tuple = tuple(current_state)
  for i in range(n):
    next_state = tuple(move(current_state, i))
    if next_state not in visited:
      visited.add(next_state)
      queue.append(next_state)
      parent[next_state] = current_state_tuple
      parent_idx[next_state] = i

As far as I remember, the initial game configuration that I encountered was the following,

$$(1, 3, 5, 7, 2, 4, 6, 8, 9, 10, 11, 12)$$.

Using our BFS traversal, the sequence of move operations with indices $i=[1, 5, 2, 3, 5]$ solves the puzzle from the initial state.

In addition, we can observe the log-scaled histogram of paths lengths (from 0 to 15).

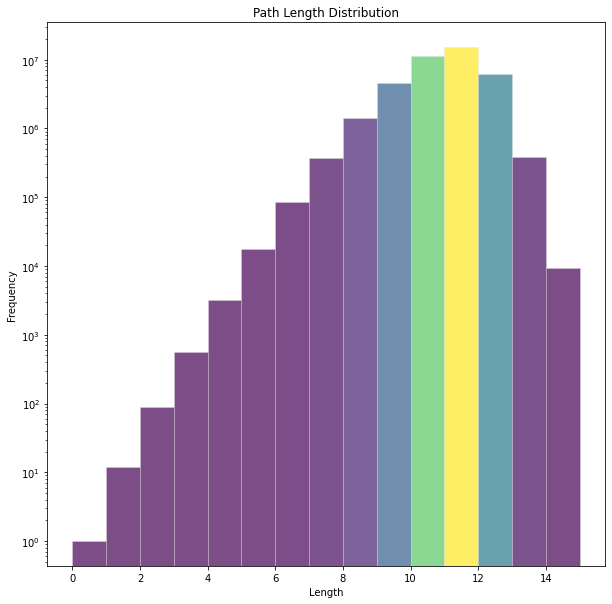
Out of curiosity, I wanted to finish this post by pointing one possible initial configuration that requires the biggest amounts of move operations is $(1, 12, 11, 10, 9, 8, 6, 7, 4, 5, 2, 3)$.

References

Turnstyle solution approach via computer search of SWAP - link
Tom’s Turnstile description and puzzle solution by J. A. Storer - link
Miller, G.A., ‘On the groups generated by 2 operators’, 1901. - link
MathOverflow discussion over genenator of Symmetric group. - link
Keith Conrad, ‘Generating Sets’ - link
Bases for permutation groups, Tim Burness, University of Bristol - link
Group Theory, J.S. Milne - link
Jeffrey S. Leon, ‘On an Algorithm for Finding a Base and a Strong Generating Set for a Group Given by Generating Permutations’ - link
Alexander Hulpke, ‘Notes on Computational Group Theory’ - link
Ken Brown, ‘Computation in permutation groups’ - link

Acknowledgment

Thanks to Niek Lamoree and Samuel Vidal for the group theory ideas and proofreading this post.