Rice

Have you ever struggled with cooking rice perfectly?

Are you tired of reading overly precise recipes like this?

For cooking 1 to 2 cups of dry rice, a 2-quart saucepan is just the right size. Too big and the rice may not steam right. Too small and it will boil over and make a sticky mess. You will add 1 3/4 cups water.

Or vague general proportions?

Add 2 parts water and 1 part rice to a large pot. For slightly firmer rice, use 1 part liquid to 2/3 parts rice.

Let us evoke the Asian wisdom, which goes beyond standard pan sizes or fancy volume unit measures.

To cook proper rice, one should add enough water to the pan so that it hits the first index finger knuckle, while the finger tip vertically touches the surface of the rice.

Let’s build up our intution and start with a set of assumptions.

# Average measurement (inches)
diameter = 6. 
height_index_knuckle = 0.8

# Conversation Rates
inch_to_cm_ratio = 2.54 
cup_water_to_cm3 = 236.588

# Random Packing Density
random_packing_density = 0.56

# Number of cups of rice to cook
rice_volume = 2 

Main assumptions:

• Random Packing Density of the grains of rice approximate one of loosely random packed spheres and it’s constant over different medium (air/water).
• The rice quality (shape) is disregarded in the analysis.

Thus, we can define our main function for the finger heuristic.

def calculate_water (pan_diameter,
                     rice_volume, 
                     height_index_knuckle = 0.8):
  '''
  Input:
    pan_diameter : float 
      Volume in inches for the pan diameter
    rice_volume : float
      Volume in cups for the rice
    height_index_knuckle : float
      Length of first index knuckle in inches

  Returns 
    Ideal water volume to add in cups
  '''
  pan_area = np.pi * ( pan_diameter * inch_to_cm_ratio )**2 / 4.0 
  volume_water_added = ( height_index_knuckle * inch_to_cm_ratio ) * pan_area 
  volume_water_added += rice_volume * cup_water_to_cm3 * (1. - random_packing_density)
  return volume_water_added * ( 1. / cup_water_to_cm3 )

We plot the results of applying our function to common sauce pan sizes and rice quantities.

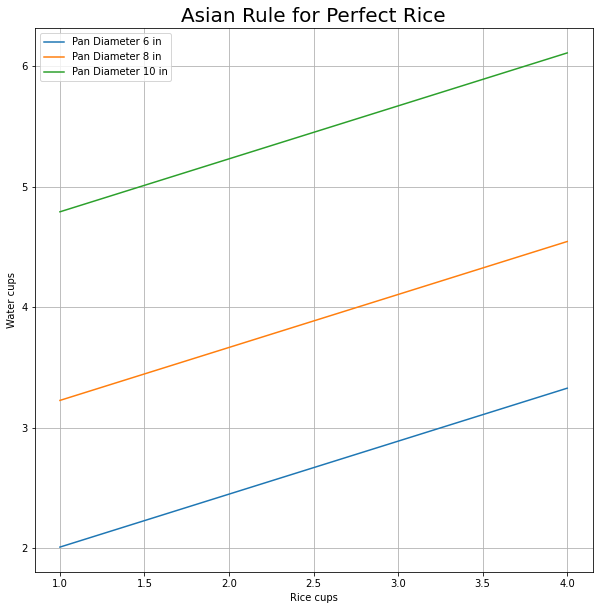
A very natural observation of the skeptic reader is: what if my finger is way smaller or bigger?

Let us consider the results from the following scientific study. Since we only care about the size of the index first knuckle, we have

Assuming independence of the variables for simplicty,

In this way, we can model the first index knuckle size distributions for simplicity as a Gaussian distribution.

mean_knuckle_size = ( 19.66 ) * (0.1 / inch_to_cm_ratio) 
std_knuckle_size = ( 2.33 ) * ( 0.1 / inch_to_cm_ratio )**2

from scipy.stats import norm
x_axis = np.linspace(mean_knuckle_size-3*std_knuckle_size, 
                     mean_knuckle_size+3*std_knuckle_size, 100)

plt.title('First Index Knuckle Distribution')
plt.plot(x_axis, norm.pdf(x_axis, mean_knuckle_size, std_knuckle_size))
plt.xlabel('inches')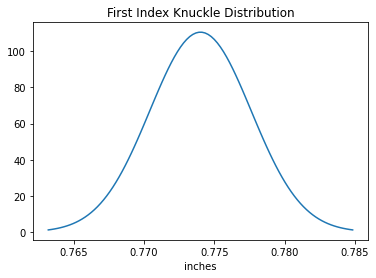

We run a MonteCarlo simulation for different size of pans, finger sizes and rice cups.

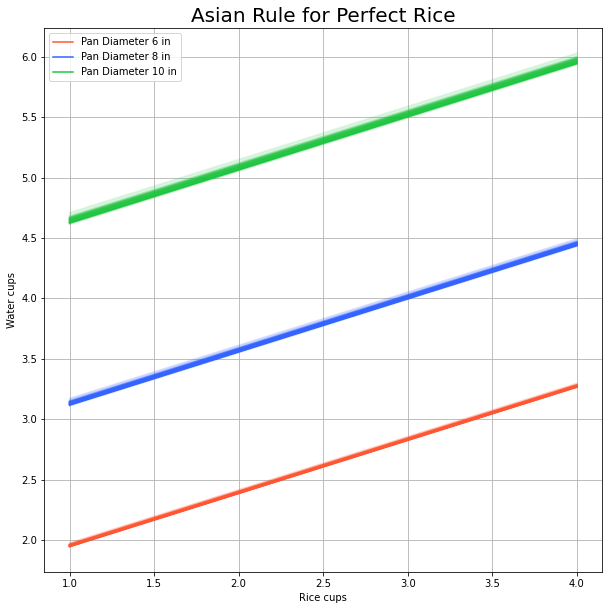
We can clearly observe that the different finger size effect is negligible in practice.

“Wisdom comes from experience. Experience is often a result of lack of wisdom.” - Terry Pratchett

References

• Common Sauce Pan Sizes - link
• Conversion Units - link
• Random Close Pack - link
• Scientific Study on Finger Sizes - link

Acknowledgment

Thanks to Raine Yeh and Pedro Bello-Maldonado for the inspiring conversation.