Power of trie-ing
In a bittersweet talk with a friend, immediately after failing a tech job interview, one unreasonable doubt came to my mind: how much memory compression can a trie actually offer? Naturally, since it was the data structure that defined my rejection, I opted to dedicate this post to it.
A trie, also known as prefix tree, is a tree data structure whose nodes store the characters present in a set of words given some alphabet (i.e., dictionary). These words can be easily retrieved by traversing down the branches of the tree.
For our analysis, we assume our alphabet size \(A\) to be \(26\), matching the English alphabet. In a simple and unoptimized manner, we could code our data structure in a few lines using Python.
class Trie:
def __init__(self):
self.children = [None for i in range(26)]
def add(self, string):
global nodes
u = self.children
for c in string:
if u[ord(c)-ord('a')] is None:
u[ord(c)-ord('a')] = Trie()
nodes += 1
u = u[ord(c)-ord('a')].childrenSince most operations on the data structure depend on the number of nodes and not on the dictionary size (key idea), I wanted to evaluate how much less characters do we need to represent a dictionary if we use a trie.
We proceed by obtaining a dictionary of english valid words and plotting their distribution by length.
import matplotlib.pyplot as plt
%matplotlib inline
from english_words import english_words_lower_alpha_set
# Set of words in english dictionary, lower case and no punctuation
S = english_words_lower_alpha_set
# Filter dataset
max_word_length = 16
S = list(filter( lambda x: '.' not in x and '&' not in x
and len(x) <= max_word_length and len(x) > 1, S))
# Plot distribution of valid words with different number of letters
lenghts = range(2,max_word_length+1)
num_words = [ len(list(filter(lambda x: len(x) == word_size, S)))
for word_size in lenghts]
fig = plt.figure(figsize=(10,7))
ax = fig.add_axes([0,0,1,1])
ax.set_title('Distribution of words by length', fontsize=15)
ax.set_xlabel('Length of words', fontsize=13)
ax.set_ylabel('Frequency', fontsize=13)
ax.bar(lenghts,num_words)
plt.show()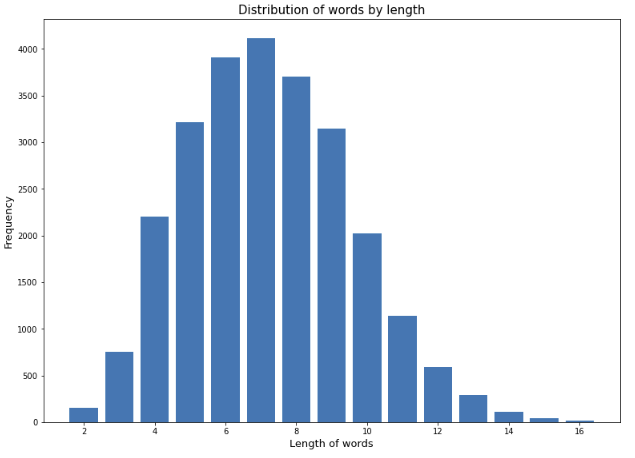
After adding each of the words of our dictionary in random order to our trie, I was truly surprised by the following results:
- Total number of chars in dictionary: 183728
- Total number of nodes of Trie to store dictionary: 77421
- General compression for storing all words in dictionary: 42.14 %
My intuition was wrong. Perhaps I was assuming that most of words in the dictionary show a more uniform distribution, causing the trie to efficiently compress short words but obtaining no memory gains on longer words. Moreover, my friend pointed out one aspect I totally overlooked: the English language has some inherent prefix structure. Most common words share a similar etimology. This observation drove my stubbornes into another experiment: random words.
We compare the memory compression rates achieved by using a trie to store the dictionary. For that purpose, we generate a multiple dictionary of random gibberish words of different lengths using the English alphabet. We compare the number of characters in total versus the number of nodes created while adding each word to the trie.
max_word_length = 16
num_chars = []
num_nodes = []
# Create random dataset of different sizes
for n in np.linspace(10, 1e6, 20):
n = int(n)
D = []
total_chars = 0
for i in range(n):
word = "".join(random.choices(alphabet_list,
k=max_word_length+1))
sz = random.randint(2,max_word_length)
D.append(word[:sz])
total_chars += sz
# Calculate global statistics after adding dictionary in trie
nodes = 1
t = Trie()
for s in D:
t.add(s)
total_nodes = nodes
num_chars.append(total_chars)
num_nodes.append(total_nodes)
# Plot trends
x = np.linspace(10, 1e6, 20)
plt.figure(figsize=(10,10))
plt.plot(x, num_chars, label = "# chars")
plt.plot(x, num_nodes, label = "# nodes")
plt.title('Memory Compression using Trie in Random Dictionary',
fontsize=15)
plt.ylabel('Memory', fontsize=13)
plt.xlabel('Number of words', fontsize=13)
plt.legend()
plt.show()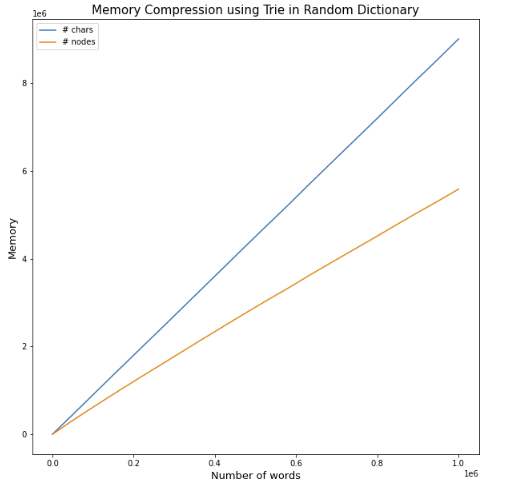
Again, my intuition was wrong :) Whenever you need to store retrieve a set of words, just use trie.